What is Practical Integrator ?
A practical integrator is an electronic circuit that performs the mathematical operation of integration on an input signal over time. It typically consists of an operational amplifier (op-amp) configured with a capacitor in the feedback loop and a resistor connected to the input. As the input signal varies, the capacitor charges or discharges, causing the output voltage of the integrator to change continuously, representing the integral of the input signal with respect to time. The output voltage of the integrator is proportional to the accumulated area under the input waveform, making it useful for applications such as signal conditioning, waveform shaping, and frequency response analysis in electronic systems.
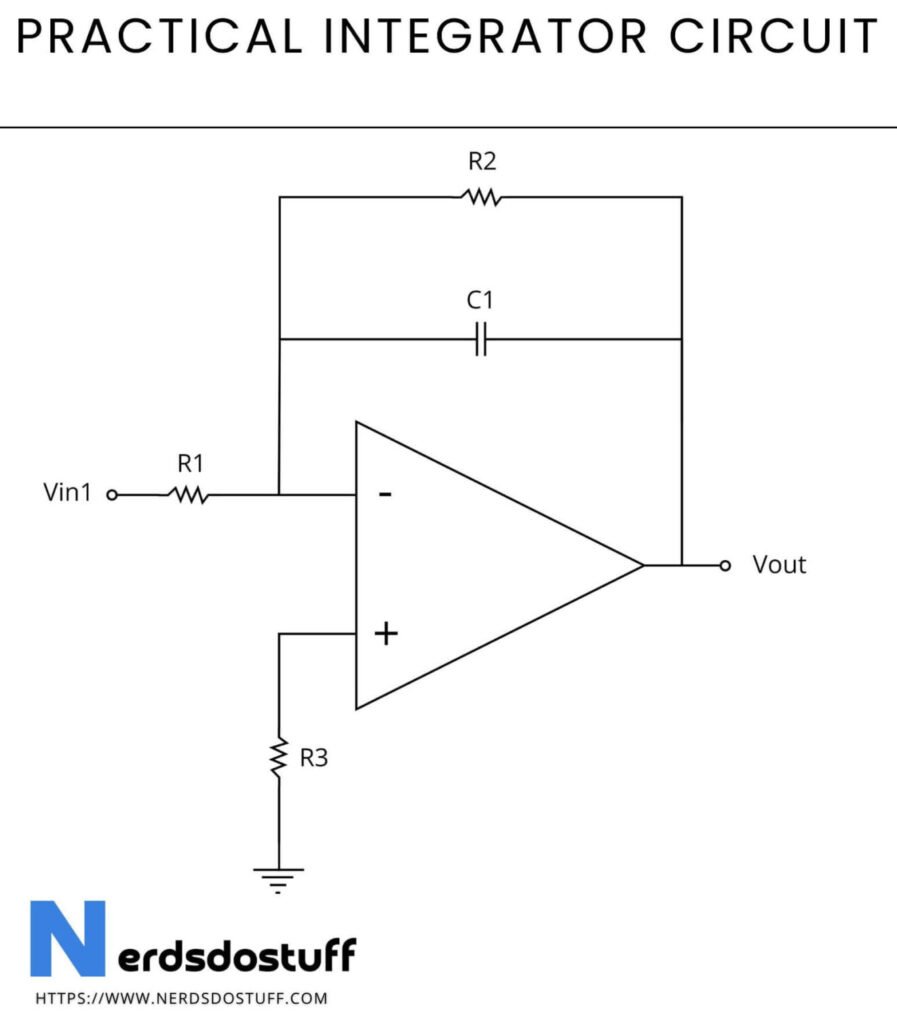
Practical Integrator Circuit
Working of Practical Integrator
A practical integrator operates by continuously accumulating the input signal over time to produce an output voltage proportional to the integral of the input signal. It typically consists of an operational amplifier (op-amp) configured as an inverting amplifier with a capacitor in the feedback loop and a resistor connected to the input. When an input voltage is applied, the op-amp amplifies the voltage across the resistor, causing a current to flow into or out of the capacitor. Since the capacitor’s voltage changes gradually according to the integral of the input voltage, the output voltage of the integrator ramps up or down over time. This behavior effectively integrates the input signal over time, making the integrator output voltage proportional to the accumulated area under the input waveform. The time constant of the circuit, determined by the values of the resistor and capacitor, determines the rate at which the input signal is integrated.
Characteristics of Practical Integrator
| Characteristic | Description |
|---|---|
| Configuration | Typically consists of an operational amplifier (op-amp) configured as an inverting amplifier with a capacitor in the feedback loop and a resistor connected to the input. |
| Integration | Performs the mathematical operation of integration on an input signal over time, producing an output voltage proportional to the integral of the input signal. |
| Output Response | The output voltage ramps up or down over time, representing the accumulated area under the input waveform. |
| Time Constant | The rate at which the input signal is integrated is determined by the time constant of the circuit, which is determined by the values of the resistor and capacitor. |
| Frequency Response | The integrator’s frequency response is determined by the cutoff frequency, beyond which the integrator’s gain decreases with increasing frequency. |
| Applications | Widely used in electronic systems for applications such as waveform shaping, signal processing, frequency analysis, and filtering. |
Applications of Practical Integrator
- Waveform Shaping: Practical integrators are used to shape the waveforms of input signals by integrating them over time. This is useful in applications such as audio processing, where integrators can be used to generate smooth changes in volume or tone.
- Signal Processing: Integrators are used in signal processing circuits to perform tasks such as differentiation, integration, and filtering. In particular, they are useful for extracting low-frequency components from input signals or removing high-frequency noise.
- Frequency Analysis: Integrators are employed in frequency analysis applications to measure the area under a signal waveform, which can provide information about the signal’s frequency content or energy distribution.
- Control Systems: Integrators are used in control systems to perform tasks such as calculating the integral of error signals in feedback loops. This helps in regulating system performance and stability.
- Instrumentation: Integrators are used in instrumentation circuits for applications such as measuring the total charge or energy in a signal waveform. This is useful in scientific experiments, data acquisition systems, and measurement instruments.
- Filters: Integrators are used as building blocks in filter circuits, where they are combined with other components to create low-pass, high-pass, band-pass, or band-stop filters. Integrators are particularly useful in active filter designs, where they provide precise control over filter characteristics.




