What is Barkhausen Criteria ?
The Barkhausen criteria was introduced by a German physicist Heinrich Barkhausen, It is a set of conditions that must be satisfied for sustained oscillations to occur in a feedback system, such as an electronic oscillator. This criteria is specifically applied to circuits that use positive feedback, where a small portion of the output signal is fed back to the input with a phase shift of 180 degrees.
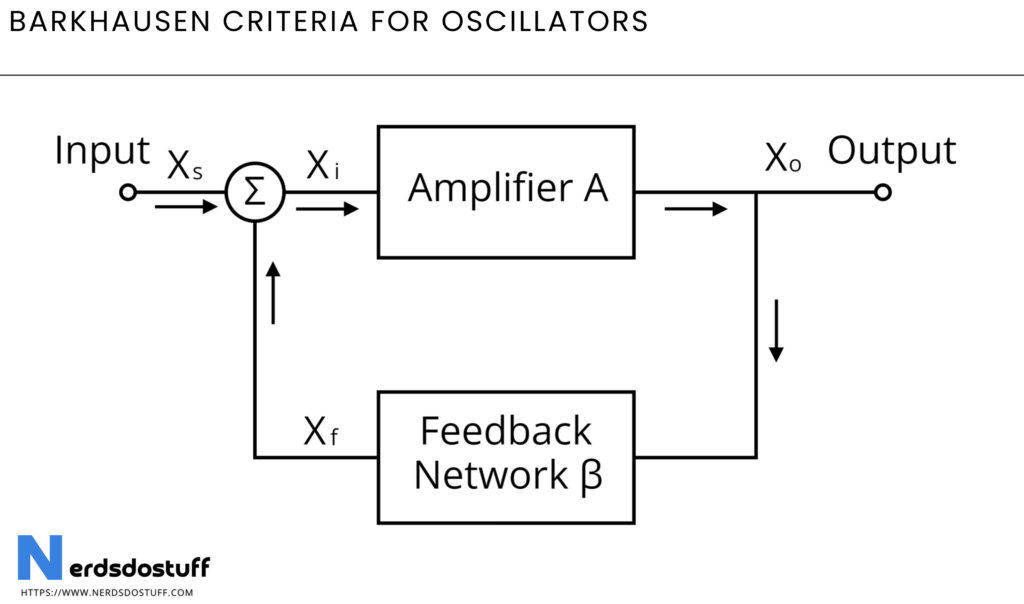
The Barkhausen criteria consist of two main conditions:
1. Amplitude Condition:
The product of the loop gain (the gain around the entire feedback loop) and the phase shift around the loop must be equal to or greater than 1.
Mathematically, this can be expressed as:
∣A⋅β∣≥1
here:
- A is the open-loop voltage gain of the amplifier.
- β is the feedback fraction (the fraction of the output voltage fed back to the input).
2. Phase Condition:
The total phase shift around the feedback loop must be a multiple of 360 degrees. This ensures that the feedback signal reinforces itself in a positive manner.
Mathematically, this can be expressed as:
Φ=360∘×n
where:
- Φ is the total phase shift around the loop.
- n is an integer (1, 2, 3, …).
When both conditions are met, the system will exhibit sustained oscillations, and the Barkhausen criteria help analyze and design oscillators and other feedback systems to ensure stability and proper functioning.
Where Barkhausen Criteria is used ?
The Barkhausen criteria is used in many electronic applications, mainly in the design and analysis of oscillators. Oscillators are circuits that generate periodic waveforms, and the Barkhausen criteria are necessary for verifying their stability and sustained oscillations. By satisfying the amplitude and phase conditions, engineers can design feedback systems that reliably produce continuous oscillations at a desired frequency. This is important in applications such as signal generators, radio frequency (RF) circuits, and audio oscillators, these applications require stable and predictable output frequency for proper functioning.
Also, the Barkhausen criteria is used in designing electronic amplifiers, especially in radio frequency and audio frequency applications. In feedback amplifier circuits, the criteria help understand the conditions under which the system becomes self-sustaining and produces amplified signals consistently. This is important for applications like audio amplification in music systems or radio frequency amplification in communication devices. Barkhausen criteria provides a balance between gain and stability in these amplifiers, ensuring optimal performance.
Barkhausen criteria is also used to understan the behavior of phase-locked loops (PLLs), a type of control system widely used in electronics for applications such as frequency synthesis, clock recovery, and demodulation. PLLs rely on feedback mechanisms, and the Barkhausen criteria helps designing PLLs that meet the necessary conditions for stable and accurate frequency control.




